Kurvenscheibe
21.07.18
hier möchte ich kurz beschreiben, wieso ich so eine komische Kurvenscheibe in meine Autos gebaut habe.
Entstanden ist diese Idee jedoch auch aus einem einfachen Stab, der an dem Bügel der Mausefalle befestigt wird. Was mir daran aber nicht gefallen hat, ist, dass nur der Durchmesser des Kreisbogens, den die Spitze des Stabes bei der Bewegung beschreibt, für die Fadenlänge wirksam ist. D.h. obwohl die Spitze des Stabes eine Kreisbahn mit großem Umfang beschreibt, bleibt am Ende doch nur der Durchmesser übrig, der zum Abwickeln einer Schnur von der Achse zur Verfügung steht. Das wollte ich verbessern.
Weiterhin hat dieser Antrieb den Nachteil, dass am Ende der Bewegung der Winkel zwischen der Schnur und dem Hebel so ungünstig ist, dass die Kräfte in der Schnur sehr groß und dafür die Wege sehr klein werden, und so der Hebel am Ende einfach nur noch umklappt ohne die Bewegung des Bügels der Mausefalle noch gut auszunutzen.
Es wird sich also über den Bewegungsbereich des Hebels die Kraft im Faden, der an der Achse zieht, ändern und auch nicht der volle Bewegungsbereich des Mausefallenbügels genutzt.

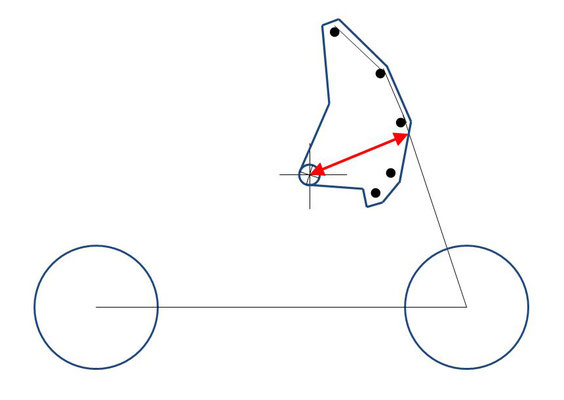
Mausefalle voll gespannt, Hebel günstig

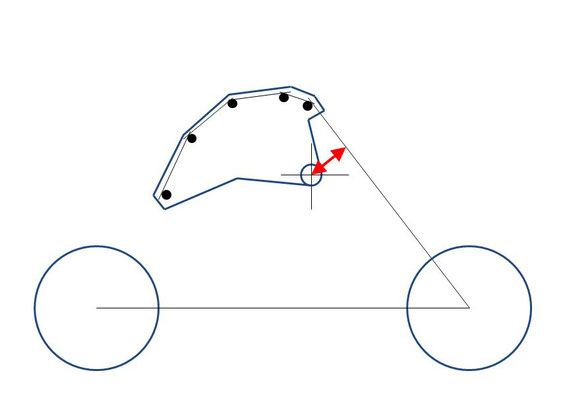
Mausefalle fast entspannt, Hebel ungünstig

Bewegungsbereich des Hebels, nur Durchmesser steht zum Antrieb zur Verfügung
Um ein Mausefallenauto möglichst weit fahren zu lassen, ist es wichtig die Kräfte der Mausefalle auf die minimal nötige Kraft an der Antriebsachse umzuwandeln. Damit das zum Einen berechnet werden kann, zum Anderen aber auch sich während der Fahrt nicht mehr ändert, ist es nötig die Kraft an der Antriebsachse möglichst konstant zu halten.
Wenn die Kraft an der Antriebsachse konstant bleibt, muss das Auto nicht ständig beschleunigt werden. Es ist dann leichter das Auto so auszulegen, dass es an jedem Punkt der Fahrstrecke immer mit der gleichen Kraft angetrieben wird und auch sicher fährt. Eine Prüfung ist dann leicht: wenn es am Anfang und am Ende fährt, dann muss es auch an jedem Punkt dazwischen fahren.
Die Mausefalle hat je nach Auslenkung ein unterschiedliches Drehmoment an dem Bügel. Dieses wird durch die Federkonstante der Wickelfeder und deren Vorspannung im "entspannten" Zustand bestimmt.
Die Kurvenscheibe hat die Aufgabe dieses, sich ändernde Moment in eine konstant anliegende Kraft an der Antriebsachse umzuwandeln.
Sie ist direkt mit dem Bügel der Mausefalle gekoppelt. Drehachse und -winkel des Bügels und der Kurvenscheibe sind gleich.
Auf diesen Skizzen sieht man schön, wie sich der Hebelarm (roter Pfeil) immer weiter verkleinert, wenn sich die Mausefalle langsam in die Endlage bewegt:
In den Bildern verringert sich von links nach rechts die Spannkraft der Feder, ebenso aber auch der Hebelarm. Daher bleibt die Zugkraft im Faden einigermaßen konstant. Man sieht auch, dass die Kurvenscheibe die ca. 180° - Bewegung des Bügels der Mausefalle mitmacht.
Wenn die Kräfte der Mausefalle in gespanntem und entspanntem Zustand ermittelt wurden, kann die Kurvenscheibe so ausgelegt werden, dass der Faden mit einer bestimmten Kraft an der Achse zieht und es kann genau berechnet werden wie weit das Auto damit fahren wird.
Da sich der Radius der Kurvenscheibe ständig ändert, ist eine Berechnung, wie weit das Auto fährt nicht ganz so einfach.
Man kann aber sehr gut näherungsweise den mittleren Radius der Kurvenscheibe für die Berechnung verwenden.
hier nochmal ein Bild einer Kurvenscheibe:
Ich habe so ein Konzept noch nie im Internet gesehen. Es wäre mir eine Freude bald viele Autos mit so einem Antrieb zu finden.
Wer dazu mehr Infos braucht, darf sich gerne an mich wenden. Ich kann zur Erstellung der Scheibe noch ein paar Tipps geben.
01.05.2019
Ich bin begeistert! Ich habe heute eine Internetseite gefunden, die ein Auto beschreibt, welches eine ähnliche Kurvenscheibe wie meines verwendet. Hier der Link zu der Seite.
Dieses Auto hat eine Weite von 138,33m damit aufgestellt. Und das scheinbar auf Turnhallenboden. Klasse Leistung!
Es hat die deutsche Meisterschaft gewonnen und es wird von einem neuen Weltrekord berichtet.
(Wo da allerdings die offizielle Rangliste steht, hab ich immer noch nicht herausgefunden.)
Es gibt also bereits Autos, die eine Kurvenscheibe einsetzen. Da die Jungs, die das Auto gebaut haben, wohl die Scheibe nicht von mir abgeschaut haben (weil sie das Auto bereits 2009 fahren ließen), freut mich das aber umso mehr.

Nachtrag 04.11.2020
mit freundlicher Genehmigung von Hr. Konrad habe ich dieses Bild auch auf meine Homepage gestellt. Das Auto hat sogar eine echte Kurvenscheibe, die kontinuierlich den Hebelarm ändert.
Respekt!
Nachtrag 14.11.2020
Es gibt noch eine Seite, auf der ein Bericht über den Wettbewerb zu finden ist, auf dem das Auto gefahren ist.
Hier wieder der Link dorthin.
25.10.2020
Nachdem ich eine Anleitung für ein Mausefallenauto mit Kurvenscheibe auf meine HP gestellt habe, möchte ich euch natürlich auch noch zeigen wie ihr selbst so eine Kurvenscheibe konstruieren könnt.
Wie die dann, nach dieser konstruktiven Vorarbeit hier, wirklich gebaut werden kann, könnt ihr ebenfalls in der Anleitung nachlesen.
Konstruktion einer Kurvenscheibe
Warum eine Kurvenscheibe ideal für große Reichweiten eines Mausefallenautos ist, habe ich auf meinen Seiten schon erwähnt.
Hier nochmal eine Zusammenfassung:
* Die Kraft einer Mausefalle ändert sich, je weiter sie gespannt wird.
* Verlängern wir den Bügel der Mausefalle einfach mit einem Stab, so ändert sich auch die Kraft am Ende des Stabes, je weiter die
Falle gespannt wird. Nach den Hebelgesetzen ist die Kraft nur kleiner als ohne Stab.
* Ein Auto mit einem Stab als Hebelverlängerung kann aber prinzipbedingt nur bis zu einem bestimmten Punkt angetrieben werden.
Danach werden die Winkel des Fadens zum Hebel so ungünstig, dass der restliche Weg ungenutzt bleibt. (siehe Stab-Konzepte).
* Ein einfacher Stab als Hebelverlängerung hält erstaunlicherweise die Kraft in einem daran befestigten Faden lange relativ konstant,
aber eben nicht so richtig gut. Auch wieder prinzipbedingt ändert sich die Kraft im Faden über den gesamten Bewegungsraum des
Hebels etwas. Das Auto wird dadurch mal etwas schneller, mal etwas langsamer fahren.
* Ein Auto, welches auf einer Bahn schneller fährt als nötig, kann seine maximal erreichbare Strecke so nicht schaffen.
Es muss immer gleich schnell fahren, wenn es maximale Reichweiten schaffen soll.
* Wir brauchen also einen "verstellbaren" Hebel, der je nach Bewegung des Mausefallenbügels seine Hebellänge ändert.
Nur so kann die Antriebskraft des Autos so gut wie möglich konstant gehalten werden.
* Einen solchen, sich ändernden Hebel, stellt die Kurvenscheibe dar.
Größe der Kurvenscheibe
Zunächst müssen wir ermitteln, welche Größe die Kurvenscheibe überhaupt haben soll.
Das ist hauptsächlich von der Art des Autos abhängig, auf die sie gebaut werden soll.
Wenn ihr ein Auto baut, welches ähnlich aufgebaut ist, wie mein Auto aus der Anleitung, so wird auch die Größe in etwa so werden, wie die der Kurvenscheibe, die dort beschrieben ist. Da muss sie nämlich um die Mausefalle herumgedreht werden können, darf daher nicht zu klein sein. Sehr viel größer darf sie aber auch nicht werden, sonst wird sie sehr schwer. Also: so klein wie möglich, so groß wie nötig.
Position auf dem Auto
für die Geometrie der Kurvenscheibe ist es nötig, dass vorher definiert wird, wo sie auf dem Auto sitzen soll.
Achtung: völlig frei kann man das nicht festlegen. Der horizontale Abstand der Mausefallenachse von der Antriebsachse, bestimmt z.B. wie groß sie maximal werden kann.
Für "übliche" Kurvenscheiben, die sich gut um die Mausefalle herumbewegen können, aber auch nicht zu groß sind, sind 200mm ausreichend. Soll die Kurvenscheibe größer werden, muss auch der Abstand vergrößert werden.
Mehr als 240mm sind da aber wohl auch nicht nötig, weil sonst die Kurvenscheiben zu groß und zu schwer werden.
Gleichzeitig muss sie etwas erhöht auf dem Rahmen sitzen. Die Kurvenscheibe bewegt sich um die Mausefalle herum und benötigt in beiden Endstellungen unterhalb der Mausefalle noch etwas Platz.
50 bis 80mm vertikaler Abstand von der Antriebsachse sollte da auch immer reichen.
Ihr merkt das bei der Konstruktion der Kurvenscheibe später, wieviel Platz sie braucht.
Blöderweise kann man sie nach der Konstruktion nicht einfach höher setzen, wenn man sie zu niedrig positioniert hat.
Die Lage der beiden Achsen zueinander definiert nämlich auch die Form der Kurvenscheibe selbst!
Man muss dann an der neuen Position eine neue Konstruktion machen.
Für die Kurvenscheibe aus der Anleitung habe ich 200mm horizontal und 58mm vertikal gewählt.
(Die 58mm kommen von der Höhe des Unterbaus. Hier habe ich einfache Leisten mit einer gegebenen Breite verwendet. Die Höhe 58mm ergibt sich dann durch das Übereinanderkleben der Leisten zu einem Lagerbock für die Mausefalle)

Hebelverhältnisse
der nächste Schritt ist die Ermittlung der Hebel, die die Kurvenscheibe haben soll.
Das richtet sich nach der Mausefalle, deren Kräfte sie korrigieren soll.
Es ist schwer die Kräfte einer Mausefalle verlässlich zu messen. Deshalb wird die perfekte Kurvenscheibe nicht beim ersten
Mal klappen. Das macht aber nichts. Wir können die erste Kurvenscheibe als erste Näherung ansehen. Die zweite, wenn überhaupt nötig, wird dann besser abgestimmt sein, wenn wir die nur noch etwas optimieren.
Die Hebelverhältnisse lassen sich relativ leicht ausrechnen. Wir brauchen uns nur um die Kräfte in den Endlagen, also in der Ruhestellung und voll gespannt, zu kümmern. Dazwischen nehmen wir an, dass die Kräfte proportional, also immer um den gleichen Betrag geändert werden, wenn sich auch der Winkel um den gleichen Betrag ändert.
Eine übliche Mausefalle hat ein Kräfteverhältnis von ca. 3:1. D.h. die Kraft in voll gespanntem Zustand ist etwa 3 mal größer als in der Ruhelage. In der Ruhelage hat eine Mausefalle bereits ca. 200 bis 250cN. Voll gespannt daher etwa 600 bis 750cN.
Die Kraft ist am Ende des Bügels, als etwa 40mm von der Drehachse entfernt gemessen.
Die absolute Kraft ist aber erstmal gar nicht so wichtig. Für die Kurvenscheibe ist nur das Verhältnis der Mausefallenkräfte nötig.
Die Kurvenscheibe hat nur die Aufgabe diese in eine konstante Kraft an der Antriebsachse umzuwandeln.
(Damit diese Antriebskraft dann so klein wie möglich wird, um möglichst große Reichweiten zu erzielen, kommen wir um ein Getriebe wahrscheinlich nicht herum.)
Wichtig dabei:
der kleine Hebel der Kurvenscheibe wirkt dann, wenn auch die Mausefalle kleine Kräfte erzeugt. Der große Hebel wirkt in voll gespanntem Zustand.
Rechnen wir uns also mal die Hebelverhältnisse kurz aus.
Wir wissen die Falle hat ein Kräfteverhältnis von ca. 3:1.
Für eine perfekte Kurvenscheibe müssen wir dann ebenfalls ein Verhältnis der Hebellängen von 3:1 anstreben.
Hier die kurze Rechnung dazu:
Ruhestellung
Die Kraft der Mausefalle ist angenommen 200cN. Wir haben uns wegen der prinzipiellen Größe der Kurvenscheibe auf einen Hebel von 70mm entschieden.
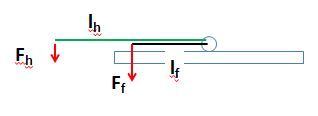
Ff = Kraft Falle
Fh = Kraft Zusatzhebel
lf = Länge Hebel Mausefalle (40mm)
lh = Länge Zusatzhebel
Es gilt nun:
Ff * lf = Fh * lh
wir berechnen die Kraft am Ende das Hebels (das wird die Kraft im Faden sein)
Nach dem Umstellen der Gleichung:
Fh = Ff * lf / lh
mit Einsetzen der Werte von oben:
Fh = 200cN * 40mm / 70mm = 114,3cN
Mit diesem Hebel haben wir also eine Kraft im Faden von etwa 114cN
voll gespannt
Jetzt müssen wir die Hebellänge ausrechnen, die wir brauchen um in dem voll gespannten Zustand ebenfalls nur eine Kraft von 114cN zu erreichen.
Das funktioniert mit derselben Gleichung von oben, nur müssen wir jetzt andere Werte einsetzen:

Ff = Kraft Falle
Fh = Kraft Zusatzhebel
lf = Länge Hebel Mausefalle (40mm)
lh = Länge Zusatzhebel
es gilt wieder:
Ff * lf = Fh * lh
Diesmal suchen wir aber die Länge des Zusatzhebels.
Wir stellen also nach lh um
lh = Ff * lf / Fh
Die Kraft der Falle ist diesmal (voll gespannt) dreimal so hoch also 600cN
Die Kraft, die der Hebel wieder erzeugen soll ist 114,3cN.
Das setzen wir in die Formel ein:
lh = 600cN * 40mm / 114,3cN = 210mm
Wir brauchen also einen Hebel von 210mm Länge um in voll gespanntem Zustand dieselbe Kraft an seinem Ende zu erhalten, wie in der Ruhestellung der Falle.
Wenn ihr jetzt das Verhältnis der Hebellängen betrachtet, werdet ihr auch ein Verhältnis von 3:1 feststellen.
Wir haben jetzt also die prinzipielle Größe der Kurvenscheibe definiert und ihr benötigtes Hebelverhältnis.
Jetzt gehts an die Konstruktion selbst.
Und weil das in Worten recht kompliziert wäre, habe ich dazu ein Video erstellt.
Das sollte euch Schritt für Schritt zeigen, wie die Kurvenscheibe erstellt wird.
Bereitet euch dazu ein großes Stück Papier (min DIN A2), Lineal und einen Zirkel vor.
Die Werte im Video und hier in der Beschreibung passen zu der Kurvenscheibe aus dem Anleitungsauto.
einziger Unterschied: Ich habe den großen Radius von 210mm auf 180mm reduziert. Die Kurvenscheibe aus der Anleitung wiegt am Ende ca. 30g. Diese habe ich zur Sicherheit in die Hebellängen mit einberechnet. Wenn ihr eine sehr leichte Konstruktion hinbekommt, ist das vielleicht nicht nötig. Das ist einer der Punkte, bei dem ihr evtl. eine zweite, optimierte Version bauen müsst, weil der erste Entwurf das Auto eben doch nicht überall gleich schnell fahren lässt. Doch zur Optimierung kommen wir dann weiter unten.
Wenn ihr eine eigene Größe definiert habt, müsst ihr deren Werte in die Konstruktion übernehmen.
Es geht dort damit los, das ihr zwei große Kreise mit den gewünschten Hebellängen als Radius zeichnet.
Dazwischen werden weitere 9 Kreise gezeichnet. Sie heben alle einen um dR unterschiedlichen Radius.
Das klingt kompliziert, ist es aber nicht.
Wir müssen den Bereich zwischen den beiden großen Kreisen aufteilen in zehn kleinere Bereiche.
Der Radiusunterschied der Kreise lässt sich dann ganz leicht berechnen:
dR = (großer Hebel - kleiner Hebel) / 10
dR = (210mm - 70mm) / 10 = 14mm.
Oder in dem Video:
dR = (180mm - 70mm) / 10 = 11mm
wichtiger Hinweis für eure Eigenkonstruktion:
Es ist wichtig, dass wir der Mausefalle eine bestimmte Position zur Antriebsachse geben müssen, ansonsten werden wir keine Kurvenscheibe konstruieren können.
Der horizontale Abstand der Mausefallenachse zur Antriebsachse darf nicht kleiner sein, als der große Radius der Kurvenscheibe.
In der Anleitung und im Video ist der große Radius 180mm und der horizontale Abstand 200mm. Wenn ihr aber eine Scheibe baut mit 240mm Radius, muss sie weiter von der Antriebsachse wegrutschen.
Außerdem muss sie etwas nach oben versetzt werden, weil die Kurvenscheibe in den Endlagen etwas unter der Mausefalle durchtaucht.
Sie bewegt sich ja um die Mausefalle herum. Das wird in dem Video auch nochmal ersichtlich.
Richtet euch bei euerer ersten Auslegung mal nach der Anleitung.
Hier nun das Video zur Konstruktion:

Frage: warum habe ich gerade 11 Tangenten, die sich in 10 Punkten schneiden, also 9 Bereiche definieren, gewählt?
Je mehr Stützpunkte man wählt, umso besser wird die ideale Kontur angenähert.
Mehr als 10 Punkte wollte ich aber nicht nehmen, weil es dann bei der Konstruktion schnell unübersichtlich wird, und die Genauigkeit dadurch auch nicht so viel weiter zunimmt. Weniger Punkte kann man selbstverständlich wählen, wenn man etwas größere Abweichungen akzeptiert. Wahrscheinlich sind weniger Punkte noch problemlos möglich.
Frage: ist die Kraft im Faden zwischen den Stützpunkten zu groß oder zu klein?

Nehmen wir beispielsweise die Kurvenscheibenposition in dem Bild an. Hier ist gerade der vierte Punkt von rechts der, der genau für diese Position ausgelegt wurde.
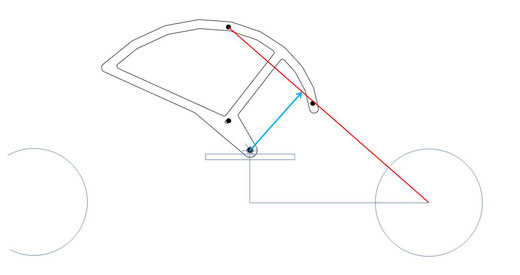
Hätten wir diesen Punkt aber gar nicht gesetzt, weil wir weniger definiert haben, so wird ein anderer Punkt gerade Fadenverlauf und damit den wirkenden Hebel definieren.
In dem Bild sind nun einige Punkte weniger zu sehen.
Die Stellung der Kurvenscheibe ist aber unverändert. Man sieht, dass der Hebel (blauer Pfeil) etwas kürzer ist.
Das heißt der Hebel ist zwischen den Punkten immer etwas zu kurz und damit die Fadenkraft etwas zu groß.
Man kann es auch so sehen: werden weniger Punkte definiert, wickelt die Kurvenscheibe weniger Faden von der Achse ab
(weil der Faden die ausgelassenen Punkte abkürzt), was am Ende die Reichweite verkürzt.
Weniger Reichweite heißt mehr Kraft.
Optimierung
wie oben bereits erwähnt, ist es nicht ganz einfach, gleich mit der ersten Kurvenscheibe eine Auslegung zu treffen, die perfekt passt.
Die Kräfte sind nicht gut messbar und z.B. das Gewicht der Kurvenscheibe selbst sind bei der ersten Auslegung kaum richtig mit zu berücksichtigen.
Nachdem ihr also schon eine Kurvenscheibe gebaut und ausprobiert habt, habt ihr festgestellt, dass euer Auto eben doch nicht überall gleich schnell fährt.
Die Optimierung für die zweite, bessere Kurvenscheibe ist jetzt nicht mehr sehr schwer.
Ihr wisst ja genau, wo das Auto schneller fährt und wo langsamer.
Fährt es gleich am Anfang schnell und wird zu Ende hin immer langsamer oder umgekehrt?
Das ist das eine was korrigiert werden kann.
Was ihr dann noch gleich mit verbessern könnt:
Als das Auto langsam unterwegs war, ist es da nur gerade so noch auf der gewünschten Strecke gefahren, oder hatte es überhaupt kein Problem und ist ganz sicher gefahren?
Ihr müsst euch jetzt nur entscheiden:
Macht ihr das Auto dort schneller, wo es langsam gefahren ist, oder macht ihr es dort langsamer, wo es schnell gefahren ist.
In beiden Fällen läuft die Konstruktion der neuen Kurvenscheibe wieder genau gleich ab, wie in dem Video beschrieben.
Ihr müsst einen der beiden Radien der Scheibe ändern. (der kleine kann je eigentlich nur noch etwas größer gemacht werden)
Annahme:
das Auto wurde zum Ende hin schneller.
(Das ist der wahrscheinlichere Fall, wegen des Gewichtes der Kurvenscheibe. Das muss am Anfang von der Falle mit hochgehoben werden, bremst also etwas, am Ende hilft es aber das Auto anzutreiben)
Gegen Ende der Fahrt wirkt ja der kleine Radius der Kurvenscheibe. Den müsstet ihr jetzt größer machen, damit das Auto langsamer wird.
Wenn das Auto im langsamen Bereich immer noch sicher gefahren ist, könnt ihr den kleinen Radius etwas größer machen. Achtung: dabei wird auch die Kurvenscheibe wieder etwas größer und damit wieder etwas schwerer.
Ihr könnt aber auch sagen, z.B. weil ihr sowieso ein Getriebe habt, was ihr noch anpassen könnt, dass ihr lieber den großen Radius kleiner macht. Damit wird das Auto am Anfang etwas schneller (es fährt dann wieder überall gleich schnell).
Damit macht ihr die Kurvenscheibe insgesamt kleiner und damit leichter. Die höhere Geschwindigkeit, die das Auto ja jetzt überall fährt, könnt ihr durch ein neues Getriebe wieder korrigieren.
Probierts einfach aus.
Es gilt immer:
Radius größer = langsamer = fährt weiter
Radius kleiner = schneller = fährt kürzer
Diese Webseite wurde mit Jimdo erstellt! Jetzt kostenlos registrieren auf https://de.jimdo.com