Auswuchtmöglichkeiten bei Mehrblatt-Rotorköpfen
bei der Analyse meiner Rotorblätter habe ich, besonders bei denen meiner Hughes, großes Unwuchtspotenzial festgestellt.
Da ich die Blätter der Hughes aber nicht auswuchten möchte, habe ich mir überlegt, ob es nur durch die Anordnung der Blätter am Rotorkopf gelingen könnte, die resultierende Unwucht aller Blätter auf ein akzeptables Maß zu bringen.
Die Berechnung von Zweiblattsystemen ist dabei recht einfach.
Am Mehrblattkopf wird der resultierende Schwerpunkt aller Blätter aber eben auch durch alle diese Blätter bestimmt.
Das heißt wir müssen die Schwerpunktlagen jedes Blattes einberechnen.
Das ist wiederum für 4-Blattköpfe einfacher als für Blattanordnungen abweichend von 90°.
Zuerst hatte ich mir ein Verfahren überlegt, welches Schritt für Schritt den Gesamtschwerpunkt berechnet.

Die Anordnung der Blätter an einem 5-Blatt-Kopf. Jedes Blatt zieht in eine andere Richtung.
Jedes Blatt mit seiner eigenen "Unwucht" bzw. Fliehkraft. m1 bis m5 soll den jeweiligen Schwerpunkt eines Blattes darstellen (hier das Ende einer Linie)

Der gemeinsame Schwerpunkt von m1 und m2 liegt etwa in der Mitte der beiden Einzelschwerpunkte und ist so schwer wie die Summe der beiden.

der gerade berechnete Summenschwerpunkt von m1 und m2 wird zur Berechnung des nächsten Schwerpunktes verwendet.
Der Schwerpunkt der Blätter m1,m2 und m3 liegt auf der skizzierten Verbindungslinie, diesmal aber bei etwa 1/3 der Stecke.

Die Berechnung geht Blatt für Blatt weiter...

...bis am Ende der Schwerpunkt aller Blätter und dessen Lage ermittelt wurde.
Man muss zuerst die Koordinaten der einzelnen Blatt-Schwerpunkte ermitteln, danach die Geradengleichungen von einem Schwerpunkt zum anderen und darüber dann jeweils die Lage der gemeinsamen Schwerpunkte....
Das Gebilde erinnert mich übrigens an die Kurvenscheibe meiner Mausefallenautos.
Dieses Verfahren erschien mir aber sehr kompliziert.
Es muss doch einen einfacheren Weg geben...?
neue Lösung Mehrblattköpfe auzuwuchten
Mir ist die Vektorrechung über Matrizen wieder eingefallen.
Jedem Blatt, bzw. dessen Unwucht kann ein Vektor zugewiesen werden.
Über dessen Koordinaten und die Summe aller x- und y-Koordinaten kann der Gesamtvektor berechnet werden.
Der ist dann ein Maß für die Unwucht des Gesamtsystems.
Die Berechnung des gemeinsamen Schwerpunktes bzw. dessen Unwuchtsvektors ist also recht einfach lösbar.
Durch die Matrizenrechnung ist die vektorielle Addition auch perfekt für Excel-Berechnungen geeignet.
Wie kann ich aber die ganzen Kombinationen, welches Blatt liegt neben welchem, berechnen und dann das Optimum herausfinden?
Es gibt insgesamt 120 Möglichkeiten die fünf Blätter an einem Rotorkopf anzuschrauben.
Die wollte ich auf keinen Fall alle einzeln durchrechnen.
Trotzdem habe ich alle Kombinationen in eine Excel-Tabelle eingetragen.
In der Berechnung habe ich mir so über die Variantentabelle eine Möglichkeit geschaffen, alle Varianten auch ausrechnen zu können.
Die 120 möglichen Varianten reduzieren sich aber eigentlich auf 12.
Es sind nämlich viele Ergebnisse doppelt in der Tabelle vorhanden:
Für den Rotor ist es am Ende egal, ob die Blätter alle zusammen genau einen Blatthalter weiterrutschen.
Auch die gespiegelten Versionen, also die Reihenfolge 1,2,3,4,5 oder 1,5,4,3,2 führt zum gleichen Ergebnis.
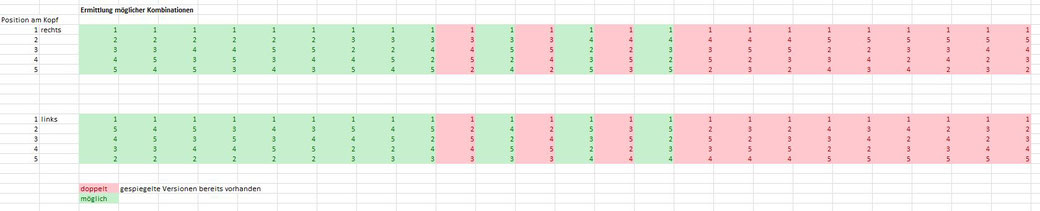
Diese Tabelle zeigt alle 24 möglichen Versionen in Relation zu Blatt 1.
Die rot markierten Anordnungen sind durch gespiegelte Versionen bereits abgedeckt. Es bleiben also nur noch 12 Kombinationen übrig.
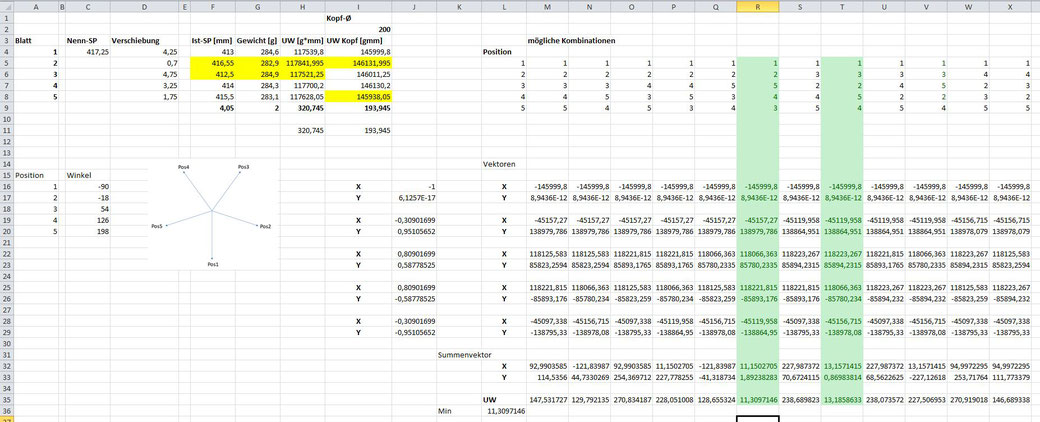
Für diese 12 Versionen habe ich dann die Excel-Berechnung durchgeführt:
Links oben sind die Blattwerte wieder zu finden.
Darunter habe ich die Winkel berechnet, unter denen die einzelnen Blatthalter am Kopf angeordnet sind.
Rechts oben sind die 12 möglichen Kombinationen aufgetragen.
Darunter findet dann die Berechnung des resultierenden Unwuchtsvektors statt. Jede mögliche Kombination der Blätter erzeugt ihre ganz "persönliche" Unwucht. Die ist in der untersten Zeile 35 eingetragen.
Wie man sieht sind die meisten Werte deutlich über 100gmm.
Es gibt aber zwei Kombinationen deren Unwucht bei gerade mal 11 bzw. 13gmm liegt.
Diese Kombinationen sind es wert ausprobiert zu werden.
Alleine durch die Maßnahme Blätter am Kopf tauschen, kann die "Unwuchtskraft" bei der Drehzahl 1160U/min von 218g auf 17g reduziert werden. Wie hier gezeigt, spielt die unterschiedliche Schwerpunktlage (Effekt 2) der Blätter keine Rolle.
Blätter ausmessen
Voraussetzung dieser Berechnung ist es, dass sowohl das Blattgewicht, als auch die Schwerpunktlage möglichst gut ermittelt wird.
Blattgewicht ist ja relativ einfach.
Die Schwerpunktlage habe ich wieder mit meiner optimierten Drahtvorrichtung gemessen.
Meiner Meinung nach ist das nur mit dieser Vorrichtung ausreichend genau möglich. Einfach über den Draht rollen und dann anzeichnen oder direkt mit dem Meterstab messen führt zu nicht ausreichend guten Ergebnissen.
Eine Alternative zur Drahtvorrichtung ist die Schwerpunktlagen erstmal sauber auf den Blättern einzustellen.
Das geht z.B. durch Auswuchten auf der Einblattwaage. Dadurch, dass dann alle Blätter zueinander ausgewuchtet sind und deren Blattgewicht bekannt ist, kann für jedes Blatt die Schwerpunktlage ausgerechnet werden.
Nachtrag 03.01.2019:
Des mit der Einblattwaage is natürlich a Schmarrn, zumindest bei einer mit Kopfabstand! Also man kann die Blätter (m*r) schon auf so einer Einblattwaage aneinander angleichen. Dann muss man aber die Schwerpunktlage auch nicht mehr errechnen, weil das Vertauschen der Blätter am Kopf dann unnötig ist. Die Blätter wurden ja bereits sehr gut aneinander angeglichen. Besser kann die Unwucht durch Vertauschen der Blätter am Kopf auch nicht reduziert werden. Ich wollte ja genau eine Methode vorstellen, bei der eben nicht gewuchtet werden sollte oder nur ein oder zwei Blätter.
Nachtrag 04.01.2019
Eine ganz „normale“ Blattwaage, bei der die Blätter miteinander verschraubt sind, ist aber durchaus verwendbar.
In diesem Fall muss das Blatt herausgesucht werden, welches das größte m*r hat, also auf der Blattwaage am „schwersten“ ist, bzw. im Vergleich zu den anderen Blättern immer nach unten geht.
Auf dieses Blatt werden alle anderen Blätter auf der normalen Blattwaage (siehe Methode "normale Blattwaage") angeglichen.
Jetzt kann grob ermittelt werden, wo der Schwerpunkt dieses Masterblattes liegt.
Alle Blätter werden so genau es geht gewogen. Damit können die Schwerpunktlagen aller Blätter berechnet werden.
Damit ist von allen Blättern Gewicht und Schwerpunktlage bekannt. m*r ist noch nicht optimal für den Verbau am Rotorkopf (Effekt 1). Damit kann durch Neusortieren der Blätter am Kopf evtl. eine Verbesserung erzielt werden.
17.12.2018
Lösungsansätze um Mehrblatt-Rotorköpfe auszuwuchten
Die Regel, mit der die Anzahl der eindeutigen Versionen V berechnet werden kann lautet V = (n-1)! / 2.
n ist dabei die Anzahl der Rotorblätter.
Jedes Blatt mehr erhöht die Anzahl der Versionen um einen Faktor, der wiederum selbst mit zunehmender Blattanzahl vergrößert wird.
n V Faktor Berechnung nächste Stufe Bemerkung
3 1 3 ------------------------------------------> daraus kann man ableiten, dass für Dreiblattköpfe keine Optimierung möglich ist
weil es nur eine eindeutige Lösung gibt. Egal wie die Blätter am Kopf angebaut
4 3 4 3*4 = 12 werden, es ist immer nur eine gespiegelte Version einer anderen.
5 12 5 12*5 = 60
6 60 6 60*6 = 360
7 360 7 360*7 = 2520
8 2520
Für den Mehrblattrotor gibt es selbstverständlich die bisher bekannten Methoden:
- Es werden wieder alle Blätter in Schwerpunktlage und -masse so gut wie möglich aneinander angeglichen. (Effekte 1 und 2 minimiert)
- Es werden alle Blätter z.B. auf der Einblattwaage in m*r aneinander angeglichen (nur Effekt 1 minimiert)
Wem, wie mir, das Auswuchten der schönen Blätter zu aufwändig, risikoreich, … ist…
Es gibt beim Mehrblattkopf ab vier Blättern nun zusätzliche denkbare Alternativen:
- Die Blätter können so am Kopf sortiert werden, dass m*r des Gesamtschwerpunktes minimiert wird.
- Es wird ein Blatt herausgesucht, welches so verändert wird, dass es eine bestimmte Unwucht hat, um m*r des Gesamtschwerpunktes zu minimieren.
- Die Kombination aus 3 und 4: erst die Blätter sortieren und dann ein Blatt suchen, welches verändert werden kann.
Anmerkungen zu den neuen Lösungen:
- Dass Rotorköpfe mit nur einem oder zwei Blättern so nicht optimiert werden können, versteht sich hoffentlich von selbst.
- Rotorköpfe mit nur drei Blättern können durch Tauschen der Blätter nicht optimiert werden. Es ergibt sich daraus immer eine gespiegelte Version (andere Montagerichtung) der Blattanordnung.
- Je mehr Blätter der Kopf hat, umso aufwändiger wird die Optimierung (weil es immer mehr Varianten gibt), umso wahrscheinlicher wird es aber auch, ein gutes Wuchtergebnis nur durch Vertauschen zu finden.
- es wird immer nur die Unwucht minimiert, die durch alle Blätter gemeinsam (Systemunwucht) gebildet wird. Die Blattschwerpunkte selbst werden dadurch nicht verändert. Der Effekt 2 bleibt also immer im Satz enthalten, so wie er in die die Blätter "hineingewuchtet" wurde. Allerdings verbessern wir mit den neuen Methoden direkt die Unwucht des kompletten Satzes auf ein Minimum. Da wir so den gesamten Rotorkopf auswuchten, wird der Effekt 1 (falls es den überhaupt gibt: es ist ja fraglich, wie die Rotorblätter vorher bereits gewuchtet waren) verbessert.
18.12.2018

Ich habe für obiges Beispiel die 12 möglichen Unwuchtsvektoren berechnet und in einer Grafik dargestellt.
Die schwarzen, dicken Linien sollen die Blattrichtungen darstellen.
Die dünnen, farbigen Linien zeigen die Richtung und Größe der Unwucht der 12 Kombinationen an.
Man kann sehen, dass, je nach Anordnung der Rotorblätter am Rotorkopf, große Unterschiede in der Unwucht des Rotors entstehen.

Für meine bisherige Anordnung gilt aus den 12 möglichen Vektoren ja nur der eine mit der Anordnung 1 (Blattreihenfolge 1,2,3,4,5). So bin ich bisher, mit dem vermeintlich gut gewuchteten Rotor, geflogen. Das Bild dazu schaut dann so aus:

Nach der Umsortierung der Blätter zu einer neuen Reihenfolge am Rotorkopf (Anordnung Nr. 6) schaut das dann in Zukunft so aus
(die ganz kleine Linie im Zentrum des Sterns):
ich habe also zufällig eine Version dabei, die sehr gute Ergebnisse erwarten lässt.
Das war die Lösung 3.
Betrachtung von Möglichkeit 4:
Hier habe ich vorgeschlagen, einfach ein geeignetes Blatt auszusuchen, das dann mit einer gezielten Unwucht versehen wird, um den Gesamtschwerpunkt zu minimieren.
Wie man aber aus dem Bild der aktuellen Anordnung 1 oben erkennen kann, ist es eher unwahrscheinlich gleich eine Anordnung zu treffen, bei der der Vektor bereits genau von einem der Blätter weg zeigt. Man wird also um ein Umsortieren der Blätter nicht herumkommen.
Was uns zu Möglichkeit 5 führt:
Hier habe ich vorgeschlagen erst zu sortieren und dann ein Blatt auszusuchen, welches gewuchtet wird.
Es kann nämlich vorkommen, dass auch beim Neusortieren der Blätter keine gute Lösung dabei ist, so dass nicht gewuchtet werden muss.
Aber es kann sich so ergeben, dass bei einer der 12 Möglichkeiten der Vektor zumindest einigermaßen von einem der Blätter weg zeigt.
D.h. man kann die Blätter dann so sortieren und das Blatt mit einem Zusatzgewicht versehen, von dem der Vektor weg zeigt.
Das wäre in obigem Beispiel V3 und V11. Die würden so aussehen:
Man sieht schön, dass der Unwuchtsvektor sehr genau in Verlängerung von Blatt 5 angeordnet ist und von diesem weg zeigt. In diesem Fall könnte man Blatt 5 etwas schwerer machen und so den Unwuchtsvektor verkleinern. Danach müsste man die Blätter neu sortieren und in der entsprechenden Reihenfolge 3 oder 11 am Kopf anordnen.
Hätte bei mir also die Lösung 3 nicht funktioniert, so hätte ich immer noch die Möglichkeit ein Blatt gezielt zu verändern, um trotzdem ein sehr gutes Ergebnis zu erreichen.
Wenn dann immer noch keine Lösung gefunden werden kann, so bleibt uns nichts anderes übrig, als entweder die üblichen Methoden anzuwenden, oder zwei Blätter gezielt zu verändern.
Diese Möglichkeit beschreibe ich hier aber erstmal nicht mehr. Das mache ich gerne, wenn bei irgendwem Bedarf bestehen würde.
22.12.2018
ich habe meine Excel-Berechnung auf 6-Blatt-Rotoren erweitert. Für den gibt es 60 eindeutige Kombinationen.
Die Excel-Berechnung ist so aufgebaut, dass von einem normalen Rotor bis zu einem 6-Blatt-Rotor alle berechnet werden können.
Wie oben bereits geschrieben, macht Blätter tauschen von 1- bis 3-Blatt keinen Sinn, trotzdem habe ich diese Versionen mit aufgenommen, weil auch hier der Unwuchtsvektor angezeigt werden kann.
Die Darstellung dieses Unwuchtsvektors hilft auch dabei das richtige Blatt herauszusuchen, das etwas schwerer (nicht das klassische Auswuchten!) gemacht werden muss, um die Systemunwucht zu optimieren.
Und so sieht die nicht gefüllte Oberfläche dazu jetzt aus:
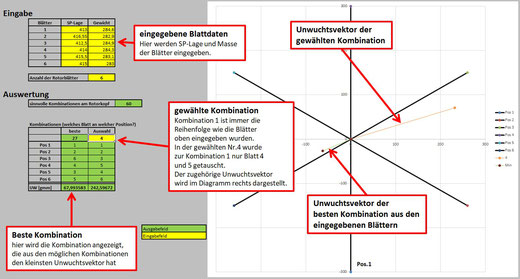
Hier sieht man das Formblatt bei Eingabe der Blattdaten eines 6-Blatt-Rotors (ohne die roten Erklärungsfelder natürlich):
Die Kombination 1 ist immer die Reihenfolge der Blätter, so wie sie in der Eingabemaske oben links eingegeben werden. Daraus berechnet Excel alle möglichen Kombinationen.
Hier wurde beispielhaft die Kombination 4 gewählt um den zugehörigen Vektor anzuzeigen. So kann aus den hier möglichen 60 Kombinationen eine ausgesucht werden, bei der der Vektor genau gegenüber eines Blattes liegt. In dem Fall kann dann das Blatt, welches bei der ausgewählten Kombination an der Position gegenüber des Vektors liegt, etwas schwerer gemacht werden und so gezielt der Unwuchtsvektor verkleinert werden.
Die Datei stelle ich gerne zur Verfügung. Ich habe nicht mehr so viele Mehrblattrotoren, die ich damit optimieren kann.
Wenn jemand Interesse daran hat, einfach anmailen. Ich kann die Datei nur per Mail zusenden.
Für die praktische Umsetzung habe ich hier noch ein paar wichtige Beispielrechungen mit eingefügt.
Hier wird beschrieben, wie man die Methode in der Praxis anwenden kann.
Diese Webseite wurde mit Jimdo erstellt! Jetzt kostenlos registrieren auf https://de.jimdo.com