einfach(e) nötige Physik

ich möchte hier wirklich nur nochmal die Grundzüge der Physik ansprechen, die für die Aufgabe des Rotor Auswuchtens wichtig sind.

Wer tiefer einsteigen möchte (oder muss), der muss sich auf anderen Seiten informieren.

Das Thema Unwucht alleine ist so umfangreich, dass es meine Seite wahrscheinlich sprengen würden. Deshalb werdet ihr für Begriffe wie "Wuchtgüte" und "Wuchtklassen" auf meiner Seite keine Erklärung finden. Ich werde die Begriffe wahrscheinlich aber auch nicht weiter nutzen.

Ich möchte dem Motto der Überschrift versuchen treu zu bleiben und wirklich nur die einfache aber notwendige Physik, die zum Verständnis der Problematik wichtig ist, und die Formeln dazu hier nochmal aufführen.

Die Physik, die zu Vibrationen am Heli-Rotor führt, kann sehr komplex sein. Der Teil davon aber, den wir herauswuchten können, ist eigentlich nicht so schwierig. Ich versuche das Thema aufbauend an den Heli-Rotor heranzuführen.

Fangen wir also erstmal relativ weit vorne an:

Das Drehmoment

Wenn man eine Radmutter lösen möchte, die zum Beispiel festgerostet ist, dann bedient man sich vielleicht eines einfachen Tricks:

Um sie zu lösen reicht die Länge des Schraubenschlüssels manchmal nicht aus. Besser: die Kraft, die ich dort aufbringen kann reicht nicht aus.

Es gibt zwei Lösungen:

Entweder wir holen uns jemanden, der mehr Kraft aufbringen kann oder wir nutzen unsere Kraft und verlängern den Schlüssel.

Wir müssen nämlich das Drehmoment so weit erhöhen, dass wir das Haltemoment der Schraube überwinden können.

Das Drehmoment (M) besteht dabei einfach aus der Kraft (F) mit der wir den Schlüssel drehen wollen und dem Abstand (r) von seiner Drehachse.

M = F * r 

Das Moment kann erhöht werden, wenn die Kraft erhöht wird oder der Abstand.

Damit wenden wir bereits das Hebelgesetz an.

Der Hebel und sein Gesetz

Der Hebel ist ein Kraftwandler. D.h. wir können auf der einen Seite mit einer kleinen Kraft an einem großen Radius am Hebel angreifen und am anderen Ende in einem kleinen Abstand zur Drehachse eine große Kraft abgeben.

(Hier zur Not auch nochmal nach mehr Infos bei anderen Quellen nachschauen.)

Solange sich der Hebel nicht bewegt (obwohl Kräfte wirken) ist das Drehmoment, das in dem Fall an dem Hebel wirkt, auf beiden Seiten der Achse gleich:

      Mlinks       =        Mrechts

Flinks * rlinks   =   Frechts * rrechts

Auch unsere Rotorblätter auf der Blattwaage sind eigentlich Hebel. Zwei gleiche Hebel, deren Kräfte sich gegenseitig aufheben sollen.

Hier wirkt einfach die Gewichtskraft der Blätter. Es gilt also das Hebelgesetz in dieser Form:

     Mlinks       =        Mrechts

 Fglinks * rlinks   =   Fgrechts * rrechts

Fg ist nun die Gewichtskraft der Blätter.

Die Gewichtskraft kann wieder durch die Masse und der Erdbeschleunigung berechnet werden:

mlinks *  glinks * rlinks   =   mrechts * grechts * rrechts

Da die Erdbeschleunigung g ja für beide Seiten gleich ist gilt folgendes:

mlinks *  g * rlinks   =   mrechts * g * rrechts

mlinks * rlinks   =   mrechts * rrechts

Man kann die Momente der Blattschwerpunkte also auch durch deren Masse und deren Abstand von der Drehachse beschreiben.

Diese Feststellung wird weiter unten bei den Fliehkräften nochmal wichtig.

Der Schwerpunkt

bevor wir auf die Waage eingehen, müssen wir uns noch kurz den Schwerpunkt anschauen.

In der Mechanik ist es oft sehr wichtig (um Rechnungen zu vereinfachen) , dass angenommen wird, dass Kräfte von Körpern, obwohl die ja eine räumliche Ausdehnung haben, nur in einem Punkt wirken. Im speziellen Fall geht es hier mal um die Gewichtskraft eines Körpers.

Die Gewichtskraft kann im Schwerpunkt angreifend betrachtet werden.

Aber oft ist es nötig, die reale Kraftverteilung zu betrachten. Z.B. bei der Schneelast eines Daches.

Dort hilft es dem Statiker wenig, wenn er die gesamte Masse des Schnees auf dem Dach so betrachtet, als wäre es nur ein extrem dichter "Schnee"-ball in der Mitte des Daches. Er muss die Flächenlast in seine Berechnungen einfließen lassen. 

Das geht an dieser Stelle jetzt aber zu weit. Weiter unten gehe ich auf Flächenlasten und deren resultierende Kraft nochmal ein. Wer mag kann sich auch die Berechnungen zu Effekt 1 und 2  ansehen. Dort habe ich die Flächenlasten der Rotorblätter genauer betrachten müssen um den Konuswinkel genau berechnen zu können. Ich gehe aber auch weiter unten nochmal auf die Flächenlast und den Schwerpunkt ein.

Wippe und Balkenwaage

´Schauen wir uns mal eine Wippe (oder auch eine Balkenwaage) an. Normalerweise haben die einen durchgehenden Balken aus einem Stück. Wir können uns den aber mal genau in der Mitte geteilt und wieder zusammengeschraubt vorstellen.

Im Prinzip gibt es dann, wie bei einem Hebel, einen linken Arm und einen rechten. Beide sind fest miteinander verbunden und haben in der Mitte eine Drehachse.

Das Bild erinnert doch schon sehr an unsere "normalen" Blattwaagen. Der Unterschied zum Hebel ist, dass die Arme jeweils gleich lang und gleich schwer sind, also keine Kraftwandlung bzw. eine 1:1 Kraftwandlung wirkt. Um die geht es aber auch gar nicht.

Nehmen wir mal an, dass es erstmal nur um das Gewicht der Arme selbst geht. Es soll noch nicht das Gewicht betrachtet werden, das normalerweise auf der Wippe draufsitzt. Weiterhin nehmen wir an, dass die Wippe reibungsfrei gelagert ist.

Wenn die Arme im Gleichgewicht sind, können wir unsere Formeln von oben wieder anwenden.

     Mlinks       =        Mrechts

Fglinks * rlinks   =   Fgrechts * rrechts

Dabei ist die Kraft F die Gewichtskraft der Arme (jeweils links und rechts der Achse aufgeteilt) und r der Abstand von der Drehachse in der die Gewichtskraft wirkt. 

Man sieht aus der Formel auch, dass es nicht zwingend nötig ist, dass r oder F auf beiden Seiten der Achse gleich ist.

Das Gleichgewicht kann auch hergestellt werden, wenn F und r links und rechts unterschiedlich ist.

einfaches Beispiel:

     Mlinks       =        Mrechts

Fglinks * rlinks   =   Fgrechts * rrechts

10N * 10mm = 5N * 20mm

100Nmm = 100Nmm

Das halb so große Gewicht ist doppelt so weit von der Achse entfernt und hält so die Waage im Gleichgewicht.

Jetzt können wir unser Bild mal so ändern, dass wir das Gewicht betrachten, dass auf der Wippe draufsitzt.

Die Wippe selbst, nehmen wir mal an, sei im Gleichgewicht oder hat kein Eigengewicht.

Das Prinzip ist das Gleiche: 

Der schwerere Vater, der auf der einen Seite der Wippe sitzt, kann durch seinen halb so schweren Nachwuchs nur im Gleichgewicht gehalten werden, wenn der doppelt so weit weg sitzt. Die Größe der Strichmännchen sollen das Gewicht symbolisieren:

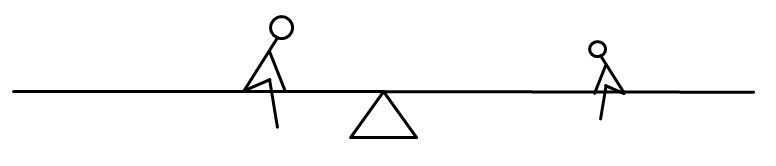
Die Bilder sind vereinfachte Darstellungen. In der Realität ist eine Wippe meistens instabil, weil die Schwerpunkte der Balken und Personen oberhalb der Achse liegen. Diesen Punkt wollen wir bei diesen Vereinfachungen mal nicht beachten. Wir müssen uns dazu also immer eine spezielle Wippe vorstellen, bei der die Balken und Menschen, die sich darauf setzen, unterhalb der Drehachse sitzen.

Aus der Formel geht aber z.B. auch hervor, dass die beiden Seiten nicht im Gleichgewicht sein müssen, obwohl sie gleich schwer sind.

Es ist immer das Produkt aus Gewicht und Abstand zur Achse entscheidend, also das Drehmoment, das die Massen an der Achse erzeugen!

Blattwaagen

Übertragen wir das Bild mal auf unsere Rotorblattwaagen:

Wir nehmen an, die Blätter sind in der Bohrung miteinander verschraubt und die Endleisten zeigen beide nach unten.

Die beiden Strichmännchen sollen jetzt das Blattgewicht und den Schwerpunkt symbolisieren

Dann haben wir wieder einen linken und einen rechten Arm (in dem Fall Blatt). Jedes Blatt hat ein bestimmtes Gewicht dessen Kraft im Schwerpunkt angreift. Dieser Schwerpunkt hat einen bestimmten Abstand zur Achse der verschraubten Blätter.

Jetzt können wir obige Formeln ganz einfach auf unsere Blätter auf der Blattwaage anwenden.

Wann sind die Blätter im Gleichgewicht?

Wenn das linksdrehende Moment gleich dem rechtsdrehenden Moment ist!

Hier sind nochmal die beiden Männchen mit den Momenten und den Kräften skizziert.

Das schwerere Gewicht auf dem linken Balken erzeugt durch den kleineren Abstand zur Drehachse ein gleichgroßes Moment wir das leichtere Gewicht auf der rechten Seite in größerem Abstand.

Da ich dieses Bild der symbolisierten Blätter in Verbindung mit den Strichmännchen auf einer Wippe sehr aussagekräftig finde. möchte ich das genau so immer wieder verwenden.

Was bedeutet es, wenn die Blätter "im Gleichgewicht" sind?

Wenn wir den Balken in Gleichgewicht bringen, heißt das nichts anderes, als dass wir versuchen den gemeinsamen Schwerpunkt der beiden Balken genau in die Drehachse der Wippe zu legen. 

Wie der gemeinsame Schwerpunkt zweier Kräfte bzw. Gewichte berechnet wird beschreibe ich weiter unten, wenn es darum geht die Schwerpunkte zu verschieben.

Gleichgewicht

schauen wir uns dazwischen kurz mal an, welche Gleichgewichtsformen es gibt.

Wenn wir von Gleichgewicht sprechen, ist üblicherweise das "stabile Gleichgewicht" gemeint.

Ein Körper ist in stabilem Gleichgewicht, wenn eine Kraftänderung von außen die Lage des Körpers zwar ändert, er mit dieser Lageänderung die von außen geänderte Kraft aber wieder ausgleicht. Im Gleichgewicht heben sich alle auf den Körper wirkenden Kräfte gegenseitig auf.

Es gibt weiterhin das "indifferente Gleichgewicht" und das "labile Gleichgewicht".

Indifferent heißt, dass es keine eindeutige Position gibt, an der ein Körper, wenn sich alle auf ihn einwirkenden Kräfte aufheben, zum Liegen kommt.

Labiles Gleichgewicht ist im Volksmund eigentlich kein Gleichgewicht. Geringste Krafteinflüsse von außen bringen einen Körper dazu seine Lage komplett zu verlassen. 

Ich hab die verschiedenen Gleichgewichtsformen während meiner Segelfliegerausbildung mit ganz einfachen Bildern erklärt bekommen:

Blätter durch Zusatzgewichte ins Gleichgewicht bringen

Angenommen wir haben einen schweren Vater auf der einen Seite der Wippe sitzen und auf der anderen wieder seinen Sohn (oder auch die Tochter). Der Vater möchte seinen Nachwuchs etwas ärgern und setzt sich etwas weiter nach hinten, so dass der Sohn auf seinem Balken einfach oben bleibt:

Der ruft nun seinen Kumpel zu Hilfe. Der setzt sich mit auf die Seite des Sohnes auf die Wippe. Er setzt sich zum Ärgernis des Vaters nun ganz außen auf die Wippe. Damit bleibt nun der Vater in der Luft:

Nun versuchen sie die Wippe ins Gleichgewicht zu bringen. Der Kumpel setzt sich nicht ganz außen auf die Wippe, sondern sucht sich genau den Platz aus, an dem die Wippe möglichst ausbalanciert ist. Das könnte z.B. so aussehen:

der ausbalancierte Zustand wäre aber auch mit einem zweiten Kind möglich gewesen, das leichter ist.

Es muss sich nur weiter außen hinsetzen:

oder es setzt sich ein weiterer Erwachsener mit drauf, der aber halt dann weiter innen:

man sieht also, dass es viele Möglichkeiten gibt, die Waage ins Gleichgewicht zu bringen. Anders ausgedrückt: an einem bestimmten Ort wird ein bestimmtes Gewicht benötigt um die Waage auszubalancieren.

Das hängt wieder mit den Drehmomenten der einzelnen Gewichte zusammen. Wie weiter oben bereits gelernt, muss nun die Summe aller Drehmomente, die im Uhrzeigersinn drehen, gleich groß sein zu denen, die gegen den Uhrzeigersinn drehen.

Ganz genauso ist es bei unseren Rotorblättern.

Auf einer Wippe erscheint das Ganze sehr logisch. Kinder wissen sehr schnell, wie das funktioniert. Man kann dort auch herumprobieren und Gewichte verschieben. Das können wir bei den Rotorblättern nun nicht so einfach. Man sieht auch nicht gleich, wie auf der Wippe, welches Blatt eigentlich das größere Gewicht hat. Man sieht nur die Reaktion auf der Blattwaage. Außerdem muss es nicht immer so sein, dass das schwerere Blatt nach unten geht. 

Es kann auch sein, dass sich die Seite der Wippe senkt, die eindeutig leichter ist:

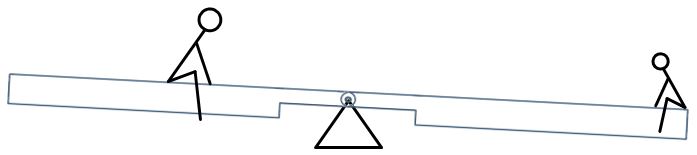
Würde man die ausbalancierten Waagen von oben jetzt in Drehung versetzen, würden sich auch die Fliehkräfte gut ausbalancieren. 

Fliehkraft und Gewichtskraft

Was hat jetzt aber die Fliehkraft unserer Rotoren mit der Gewichtskraft von Wippen und Hebeln zu tun?

Die Fliehkraft und die Gewichtskraft wirken doch in komplett unterschiedliche Richtungen?

Das stimmt natürlich. Aber beide werden vom Schwerpunkt (Lage und Masse) bestimmt.

Und wenn das Drehmoment, das die Gewichtskraft auf der Blattwaage erzeugt, bei beiden Balken gleich ist, dann ist auch die Fliehkraft, die dann bei einer Drehung entsteht bei beiden Balken gleich.

Das heißt, dass wir uns die Gewichtskraft zunutze machen können, um die später bei Rotation auftretenden Fliehkräfte zu optimieren.

Die Gewichtskraft entsteht durch eine Beschleunigung der Masse in Richtung Erdmittelpunkt, die "Fliehkraft", dadurch, dass die Masse von ihrer geraden Bahn abgelenkt wird.

Der Schwerpunkt der Blätter wird immer nach innen in eine andere Richtung gezogen und möchte aber eigentlich auf einer geradlinigen Bahn weiterlaufen. Dadurch entsteht die Zentripedalkraft. Sie ist nötig um den Schwerpunkt aus seiner geraden Wunschbahn heraus in eine Kreisbahn zu zwingen.

Das heißt nun nochmal folgendes: wenn die Blätter auf der Blattwaage im Gleichgewicht sind (es wirkt die Gewichtskraft), dann sind sie es auch am bei der Drehung (es wirkt die Fliehkraft). Zumindest, wenn wir sonst am System nichts ändern! Das das aber in der Realität gemacht wird zeige ich später noch.

Damit haben wir das einfache Prinzip, wie das Rotorblattauswuchten funktioniert aber eigentlich schon erklärt.

Weiter unten kommen aber noch ein paar Details, weshalb es eben doch nicht ganz so einfach ist.

Fliehkräfte

gerade haben wir gehört, dass die Fliehkraft der Rotorblätter ebenso durch die Masse und dem Radius des Schwerpunktes bestimmt wird, wie das Moment, das die Blätter auf der Waage ausbalanciert.

Bei unseren Rotoren geht es ja eigentlich nicht darum, dass irgendein linksdrehendes Moment der Blätter gleich einem rechtsdrehenden Moment ist. Es geht darum, dass sich die Fliehkraft des einen Blattes genau mit der des anderen Blattes aufhebt.

Oder, dass sich die Fliehkräfte aller Blätter genau aufheben.

Wie entsteht die Fliehkraft?

Die Fliehkraft ist die Kraft, die benötigt wird einen Massenpunkt aus seiner geradlinigen Bahn in eine Kreisbahn zu zwingen.

Sie ist von der Drehzahl, von der Masse des Objektes und von dessen Kurvenradius abhängig.

In einer physikalischen Formel schaut das so aus:

F = m * r * w²

w (Omega) ist dabei die Winkelgeschwindigkeit. Darauf will ich hier aber gar nicht weiter eingehen. Wir wollen bei einfacher Physik bleiben. Dazu gibt es genügend Infos im Internet. Wir wollen ja auch die Kräfte nicht ausrechnen, wir wollen sie nur vergleichen.

Es soll jetzt also folgendes bei unseren Rotoren gelten:

F_Blatt1 = F_Blatt2

F1 = F2

m1 * r1 * w1 = m2 * r2 * w2

da w definitiv für alle Rotorblätter am Kopf gleich ist, gilt folgendes:

m1 * r1 * w = m2 * r2 * w

m1 * r1 = m2 * r2

kommt uns diese Formel nicht bekannt vor?

Da steht jetzt doch wieder ein Moment, eine Kraft (oder besser die Masse, die auch die Gewichtskraft der Blätter erzeugt) mal einem Hebelarm.

Genau das ist der Grund, weshalb wir die Rotorblätter auf der Blattwaage auswuchten können und weshalb die Gewichtskraft der Blätter auf der Blattwaage uns hilft die Fliehkräfte am Rotorkopf angleichen zu können.

Feinheiten

Angenommen wir haben wieder eine Wippe (weil es so einfacher zu verdeutlichen ist), die schön ausbalanciert ist.

Die Masse auf dem linken Balken ist doppelt so schwer wie die auf dem rechten, dafür ist sie nur halb so weit vom Drehpunkt entfernt:

Wie oben gelernt wird dieses System auch bei Drehung ausbalanciert sein, d.h. auch die Fliehkräfte sind ideal ausgeglichen.

Wenn wir jetzt die Balken an der Wippe abmontieren (die Personen bleiben genau da sitzen, wo sie gerade sind!) und ein Zwischenstück einbauen, schaut das ganze vielleicht so aus:

Wenn wir die Wippe nun loslassen wird sie weiterhin im Gleichgewicht sein?

Schauen wir uns das mal genauer an:

Vor dem Ummontieren galt folgendes:

Fg_Mann * X = Fg_Kind * 2* X

2*m * g *  X = m * g * 2 * X

M_links = M_rechts = M

Die Wippe war also genau im Gleichgewicht.

Nach dem Ummontieren gilt jetzt das hier:

M_links =

= Fg_Mann * (X + a) = 

 = 2*m*g*(X+a) = 

= 2*m*g*X  + 2*m*g*a

2*m*g*X war aber ja das Moment M vor dem Umbau. Das setzen wir nun wieder ein:

M_links = M+2*m*g*a

m*g*a ist ein Moment, das durch die Abstandsänderung an der Wippe erzeugt wird.

Bezeichnen wir das mal als M_Abst.

M_links = M+2*M_Abst

analog für M_rechts:

M_rechts =

= Fg_Kind * (2 * X + a)

 = m*g*(2*x+a) =

 = m*g*2*X + m*g*a

mit M = 2*m*g*X (vor dem Umbau) gilt: 

M_rechts  = M+m*g*a

mit m*g*a = M_abst gilt wieder analog:

M_rechts = M+M_Abst

M_links =  M + 2*M_abst       und       M_rechts = M + M_Abst

Das heißt, dass in dem Beispiel oben, auf der linken Seite ein Moment hinzukommt, das doppelt so groß ist, wie das auf der rechten Seite.

Damit ist die Wippe nicht mehr im Gleichgewicht. Sie wird sich auf der linken Seite senken!

Wie groß der Unterschied des Momentes ist, das bei einer Abstandsänderung hinzukommt hängt vom Gewichtsunterschied bzw. dann damit vom Abstand der Schwerpunkte von der Achse ab und natürlich von der Abstandsänderung selbst ab.

In unserem Spezialfall im Beispiel oben war das Kind ja gerade halb so schwer wie der Erwachsene. Deshalb ist der Unterschied auch genau Faktor 2.

Übertragen wir das Bild wieder auf unsere Rotorblätter:

Wir wuchten auf der Blattwaage oft so, dass die Blätter miteinander verschraubt sind.

Danach schrauben wir die Blätter am Rotorkopf mit Abstand fest.

Wenn nun die Schwerpunkte der Blätter nicht exakt an der gleichen Stelle liegen, erzeugen wir wieder ein Ungleichgewicht der Fliehkräfte.

Das habe ich auf meiner Homepage  mit Effekt 1 Transferfehler bezeichnet. 

Es gibt zwei Lösungen um den Fehler zu beseitigen:

Lösung 1:

Wir haben weiter oben festgestellt, dass es viele Möglichkeiten gibt, den schweren Teil der Wippe auf der anderen Seite auszugleichen. Genauer gesagt, gibt es davon unendlich viele. Jeweils für beide Varianten, mit und ohne Abstand, gibt es jeweils unendlich viele Kombinationen aus Gewicht und Ort. Aber es gibt nur genau eine Möglichkeit die sowohl die Balken ohne Abstand, als auch die mit Abstand verschraubten Balken ins Gleichgewicht bringt. Und genau die möchte ich rechnerisch mal vorstellen. 

Die Formeln von oben kennen wir noch. Daran hat sich nichts geändert. Das Moment, das linksherum dreht muss immer noch genau so groß sein, wie das Moment, das rechts herum dreht. Nur rechnen wir das jetzt etwas allgemeiner durch:

Angenommen wir kennen folgende Werte:

Masse des Balkens links m_l und dessen Schwerpunktlage X_l

I)

M_links = M_rechts

Fg_l * X_l = Fg_r * X_r

m_l * g * X_l = m_r * g * X_r      beide Seiten /g

m_l * X_l = m_r * X_r

Gleichzeitig soll das aber wieder mit dem Abstandsstück (a) zwischen den Balken gelten:

II)

m_l * (X_l + a) = m_r (X_r + a)

m_l * X_l  + m_l * a  =  m_r * X_r  + m_r * a

subtrahieren wir die beiden Gleichungen

Gl.II - Gl.I 

    m_l * X_l  + m_l * a  =  m_r * X_r  + m_r * a

 -  m_l * X_l                  =  m_r * X_r

folgt:

m_l * a = m_r * a

m_l = m_r

die beiden Gleichungen können also nur gleichzeitig eingehalten werden, wenn die beiden Massen links und rechts auch gleich sind. 

Wenn die beiden Massen gleich sind, dann sind auch die jeweiligen Schwerpunktlagen gleich (im ausbalancierten Zustand der Wippe!).

Wenn wir also auf der Blattwaage auswuchten wollen und den Transferfehler zur Montage am Rotorkopf vermeiden wollen, dann muss das Gewicht links und rechts der Blattwaage gleich und ausbalanciert sein.

Diese Lösung streben viele Wuchtmethoden an:

- bisherige Methoden: iteratives Angleichen und Drahtmethoden

- alternative Methoden: Drahtmethode und gezielt Wuchten

Es gibt aber noch eine andere Lösung. Auf die gehe ich aber erst später nochmal ein.

Siehe weiter unten bei zweite Lösung 2.

Leichterer Balken senkt sich???

Es ist also erstmal unser großes Ziel, den Balken links und rechts der Achse gleich schwer zu machen.

Was machen wir, wenn das Ganze so aussieht, wie auf dem nachfolgenden Bild?

Hier senkt sich der leichtere Balken, weil sein Schwerpunkt ausreichend weiter außen liegt um das schwerere Gegengewicht hochzuheben.

Wir sollen aber ja die Balken gleich schwer machen. Wenn wir das tun, wird sich aber der Balken, der eh schon unten ist, noch deutlicher senken wollen, bzw. der Unterschied der Fliehkräfte noch größer. In der Realität unserer Rotorblätter ist das übrigens ganz normal.

Es wird sich oft das leichtere Blatt auf der Blattwaage senken.

Ich möchte hier keine mathematischen Berechnungen dazu durchführen. Ich möchte das nur hier mit aufführen, weil es wichtig ist das zu wissen. Die meisten Anleitungen gehen darauf nicht ein, aber sie lösen das Problem dadurch , dass angestrebt wird das Blattgewicht gleich zu machen, trotzdem.

Im Prinzip muss das leichtere Blatt durch Zusatz-Gewicht erst zum Schwereren gemacht werden und das wird dann auf der anderen Seite wieder ausgeglichen.

Ich habe das mal versucht mit den Wippen-Bildern darzustellen. Diesmal habe ich die Schwerpunkte mit eingezeichnet. Es ist nur eine Skizze. Die Größen und Lagen der Strichmännchen sind nur grob dargestellt.

Die roten Strichmännchen stellen die Zusatzgewichte dar, die wir durchs Auswuchten aufbringen müssen.

Bild 1 zeigt die Ausgangssituation, leichteres Blatt senkt sich:

Bild 2:

Hier hilft nur, den leichteren Balken (Blatt) zum Schwereren zu machen und dass am Besten gleich so, dass der gemeinsame Schwerpunkt am Ende genau da liegt, wo er am anderen Balken auch liegt. 

Das erledigt die Drahtmethode, und hier die optimierte Version davon, sehr einfach. Aber auch meine Excel-Berechnung „gezielt Wuchten“ bringt genau an der richtigen Stelle Gewicht auf, um den Schwerpunkt gezielt zu verschieben

Die Schwerpunktlagen sind nun schon mal gleich, aber die Blätter sind noch unterschiedlich schwer. Deshalb bleibt das rechte Blatt weiter gesenkt.

Bild 3:

Danach kann das nun leichtere andere Blatt in dessen Schwerpunkt genau gleich schwer gemacht werden.

Das geht dann auf jeder Blattwaage ganz leicht.

Nach diesem Wuchtvorgang müssen die beiden Blätter möglichst genau gleich schwer sein und möglichst gut ausbalanciert sein.

Warum aber wurde eigentlich der Schwerpunkt des rechten Blattes verschoben?

Resultierende zweier Kräfte bzw. wieso wird der Schwerpunkt verschoben?

Auf der Wippe erscheint das Bild wieder ganz logisch: Setzt man zu dem Kind auf dem leichteren Balken noch einen Erwachsenen weiter innen, so wird der Balken zwar schwerer, aber seine Gewichtskraft greift jetzt auch woanders an. Schauen wir uns das mal genauer an:

Bild 1

Hier ist ein Balken gegeben, dessen Schwerpunkt von dem Kind beschrieben wird. Würden wir diesen Balken alleine auswiegen (wieder eine Wippe), so wäre er jetzt im Gleichgewicht. (Immer vorausgesetzt, dass ignoriert wird, dass eine Wippe prinzipiell immer instabil ist)

Bild 2

Wird jetzt ein Erwachsener genau in demselben Punkt mit auf den Balken gesetzt, wird sich am Gleichgewicht, also an der Schwerpunktlage, nichts ändern. Aber der Balken ist schwerer geworden.

Bild 3

Setzt sich jetzt ein Erwachsener an den Rand, wird jedem klar sein, dass der Balken kippt.

Bild 4

Der Balken oder die Achse muss jetzt verschoben werden um wieder im Gleichgewicht zu sein. Dort, wo dann die Achse liegt, ist der neue Schwerpunkt. Wir haben durch das zusätzliche Gewicht den Balken wieder schwerer gemacht, aber gleichzeitig den Schwerpunkt verschoben.

Genau das können wir nun nutzen um die Balken bzw. unsere Rotorblätter aneinander anzugleichen.

Die Kunst ist genau das richtige Gewicht an die richtige Stelle zu setzen um das gewünschte Ergebnis zu erhalten.

Wie wird nun berechnet, wie weit sich der Schwerpunkt verschiebt?

Angenommen wir haben einen Balken mit einem bestimmten Gewicht und einer bestimmten Schwerpunktlage.

Und nehmen wir, der einfacheren Betrachtung wegen, erstmal weiter an, dass der an einer Seite befestigt ist (einseitig eingespannter Balken)

Diesen Ort habe ich gewählt, weil die Schwerpunktlagen der Blätter ja meistens von der Blattschraube aus gemessen werden.

Dann erzeugt sein aktueller Schwerpunkt ein bestimmtes Moment an der Einspannung.

M = Fg * X

Wird nun ein zusätzliches Gewicht irgendwo aufgebracht, so erzeugt dieses auch ein zusätzliches Moment an der Einspannung.

M_zus = Fg_zus * X_zus

In Summe ist nun das Moment an der Einspannung:

M_ges = M + M_zus

Das interessiert uns ja aber eigentlich gar nicht. Wir wollten ja wissen, wo der neue gemeinsame Schwerpunkt liegt.

Das lässt sich nun so berechnen:

M_ges = Fg_ges * X_ges

Damit wird die obige Gleichung zu dieser hier:

Fg_ges * X_ges = M + M_zus

Fg_ges kennen wir ja. Wir wissen, wie schwer der Balken vorher war und wir wissen, welches Gewicht wir aufgebracht haben.

Was wir suchen ist ja eigentlich X_ges

Das lässt sich nun aus der Gleichung ausrechnen:

X_ges = (M + M_zus) / Fg_ges

Setzen wir die Kräfte und Abstände wieder ein:

X_ges = (Fg * X + Fg_zus * X_zus) / Fg_ges

X_ges = (Fg * X + Fg_zus * X_zus) / (Fg +Fg_zus)

Jetzt haben wir den neuen Ort der gemeinsamen Massen des Balkens ausgerechnet.

Genau diese Formeln habe ich in meiner Berechnung „gezielt Wuchten“ angewendet.

Man kann so auch ausrechnen, welches Gewicht wo aufgebracht werden muss, um eine definierte Schwerpunktlage zu erreichen.

Dazu muss die Gleichung nur nach Fg_zus umgestellt werden:

Fg_zus = Fg * (X - X_zus)/(X_ges - X_zus)

Eine Alternative ist, genau das Differenzgewicht der beiden Balken an die richtige Stelle zu setzen. Damit wäre in einem Schritt sowohl das Gewicht, als auch die Schwerpunktlage der beiden Balken angeglichen.

Das Problem dabei ist, dass das nur selten funktioniert. Die Balken haben ja nur eine begrenzte Länge auf denen das Gewicht platziert werden kann. Und dabei kann es eben vorkommen, dass es außerhalb der Balken platziert werden müsste.

Lösung 2:

Oben habe ich kurz angemerkt, dass es noch eine zweite Lösung gäbe, um den Transferfehler zu umgehen.

Die ist eigentlich ganz einfach. Man darf eben den Abstand bei der Montage am Rotorkopf nicht mehr ändern. Das bedeutet, dass die Blattwaage eben genau den Abstand haben muss, der später am Rotorkopf auch vorhanden ist.

Da nun nur eine Gleichung eingehalten werden muss (weil die Gleichungen auf der Blattwaage und dem Rotorkopf gleich sind) gibt es jetzt wieder unendlich viele Möglichkeiten einen Gleichgewichtszustand und damit ausgeglichene Fliehkräfte herzustellen.

Diese Lösung ist mit der Methode "Einarm Blattwaage mit Kopfabstand" unter den alternativen Vorschlägen gut durchzuführen.

Da diese Lösung nicht darauf abzielt, die Blätter gleich schwer zu machen (und damit auch nicht die Schwerpunktlagen) kann es aber andere negative Effekte geben (Effekt 2 und Voraluf). 

Das habe ich unter Berechnungen zu Effekt 1 und 2 und unter zusätzliche Optimierungen/Vorlauf genauer beschrieben.

Es gilt denn wieder:

M_links = M_rechts

Fg_l * (X_l + a) = Fg_r * (X_r + a)

m_l * g * (X_l + a) = m_r * g * (X_r + a) 

m_l * (X_l + a) = m_r * (X_r + a)

Jetzt kann man aber analog den Wippenbildern wuchten wo man möchte. Sinn macht es da evtl. ganz außen nur wenig Gewicht aufzubringen um die Blätter ins Gleichgewicht zu bringen:

Flächenlasten und deren Resultierende

Bisher haben wir die Balken der Wippe immer recht einfach dargestellt und nur deren Masse und die Lage des Schwerpunktes betrachtet.

Eigentlich haben die Balken aber ja eine Länge. Wie kommt man nun auf die Schwerpunktlage? Woher wissen wir, wo der Schwerpunkt eines Balkens liegt?

Hier noch eine kurze Erklärung dazu, weil das Thema bei den Fliehkräften nochmal aktuell wird.

Wieder mal ne Annahme: Auf einem Dach liegt Schnee. Überall gleich hoch und gleich dicht.

Das ist logischerweise eine bestimmte definierte Menge. Man kann also genau bestimmen, wie schwer der Schnee ist.

Aber… der liegt ja nicht in einem kleinen Punkt auf dem Dach, sondern über die ganze Fläche verteilt.

Wie soll nun der Statiker berechnen, wie das Dach konstruiert werden muss, so dass es die Schneelast aushält?

Er rechnet nicht mit dem Kraftangriffspunkt der gesamten Last in einem Punkt.

Er rechnet mit der Flächenlast.

Im Prinzip wird die gesamte Schneemenge in kleine Abschnitte aufgeteilt. Ganz viele senkrechte, quadratische Säulen.

Jede Säule ist so hoch wie die Schneedecke vorher war und hat nur eine kleine quadratische Grundfläche.

Von jeder Säule kann man wieder berechnen, wie schwer sie ist. Alle zusammen ergeben dann wieder das Gesamtgewicht.

Die ganzen Säulen sie nun über das Dach verteilt und belasten es anders, als wenn es nur ein Punkt wäre, der irgendwo in der Mitte angreift.

Aber aus der ganzen Verteilung über das Dach kann man natürlich auch berechnen, wo die Gesamtkraft angreift und wie groß sie ist. Diese Gesamtkraft ist die Resultierende.

Der Vorteil davon ist, dass es eigentlich egal ist, ob der Schnee überall gleich hoch ist. Jede Verteilung auf dem Dach kann dabei berechnet werden. Die Verteilung mit gleicher Höhe ist dabei nur die einfachste Variante.

Bleiben wir mal zweidimensional. Auch hier kann man die Flächenlast bzw. die Resultierende daraus berechnen.

Das wäre dann vielleicht eher unser Balken der Wippe. Der hat auch eine Länge, wie die Schneedecke, aber eine vernachlässigbare Tiefe.

Wenn der Balken überall gleich dick (und gleich dicht ist), ist sein Gewicht über seine Länge gleichmäsig verteilt:

Die Resultierende Fq wird jetzt eigentlich über die Integralfunktion berechnet.

Man kann sie aber auch annähern indem man die Fläche in Abschnitte aufteilt.

Für unseren Balken (bzw. die Schneedecke auf einem Dach) ist die Berechnung recht einfach:

Fq = L * H

X_Fq =  L / 2

Je kleiner die Abschnitte und je mehr es werden, umso näher liegt man an der genauen Kurve.

Die Gesamtkraft Fq entspricht der Fläche unter der Kurve, jede einzelne Kraft F1, F2,... entspricht der Fläche der entsprechenden Säule.

In meiner Berechnung zu den beiden Effekten habe ich 100.000 Abschnitte berechnet.

Genau kann man das mit der Integralfunktion ausrechnen, aber ich wollte ja bei einfacher Physik bleiben.

Unsere Rotorblätter sind zum Einen der Auftriebskraft zum Anderen den Fliehkräften ausgesetzt.

Wenn man unsere Rotorblätter in solche Abschnitte aufteilt, wie sie in den Skizzen oben dargestellt sind, kann man sowohl die Auftriebskraft als auch die Fliehkraft in jedem Abschnitt betrachten und berechnen.

Dabei stellt man fest, dass beide Flächenlasten sind, die sich über die Länge des Rotorblattes ändern.

Damit sind dann auch die Kraftangriffspunkt klar definiert, welche für beide (Auftriebs, und Fliehkraft) eben nicht der Schwerpunkt ist.

Wieso wird nun das Blatt leichter oder warum greift die Fliehkraft nicht im Schwerpunkt an?

Die Fliehkraft kann zum einen, wie allgemein üblich, über Schwerpunkt (Masse und Lage) berechnet werden, als auch wie hier gezeigt über die Summe der Einzelabschnitte berechnen und eben der resultierenden Kraft daraus.

Da die Fliehkraft nach beiden Berechnungsmethoden dieselbe ist, sich in der Realität aber der Kraftangriffspunkt wegen der Dreiecksverteilung weiter außen befindet, muss das Blatt in der Realität, zumindest für die Fliehkraft, leichter geworden sein. 

Das ist natürlich nicht der Fall! Das Blatt hat immer noch die gleiche Masse. Diese Masse unterliegt aber einer Beschleunigung.

Ähnlich wie im Gravitationsfeld der Erde, erfährt eine rotierende Masse eine Beschleunigung. Und ähnlich wie beim Gravitationsfeld muss die nicht überall an dem Körper gleich sein.

In unserem Fall wird das Rotorblatt in der Nähe des Schwerpunktes, den es in Ruhe hat, einer Beschleunigung von ca. 1000g ausgesetzt. Das an sich ist aber noch nicht die Ursache für die Dreiecksverteilung der Fliehkraft. Vielmehr ist es die Tatsache, dass sich die Beschleunigung über die Länge des Blattes stark ändert. Weiter innen ist es deutlich weniger, weiter außen deutlich mehr. Deshalb verschiebt sich der Angriffspunkt der Fliehkraft des Blattes an die Stelle weiter außen am Blatt. Der Massenschwerpunkt bleibt natürlich an der gleichen Stelle. Die Teile, die sich weiter außen befinden, wirken nur schwerer als die, die weiter innen sind. 

Die Fliehkraft ändert sich dabei linear über die Ausdehnung des Körpers.

Die Lage der Resultierenden ist von dem Abstand des Schwerpunktes von der Rotationsachse, der Ausdehnung des Körpers und von seiner Rotationsgeschwindigkeit um die Achse abhängig.

Sie entsteht aus einem konstanten Anteil (Rechtecksanteil der Kurve) und einem linearen (Dreiecksabschnitt der Kurve ). Die beiden Resultierenden dieser Anteile werden überlagert, d.h. die beiden Kräfte werden zu einer Gesamtkraft verrechnet. Die Kurve ist eine abgeschnittene Ursprungsgerade

Wo die Resultierende genau liegt hängt also davon ab, wie stark sich die Fliehkraft über die Ausdehnung des Körpers ändert.

Bei einem Satelliten, der um die Erde fliegt, ist der Dreiecksanteil der Kurve vernachlässigbar. Hier überwiegt der Rechteckanteil der Kurve und deshalb greift die Fliehkraft näherungsweise im Massenschwerpunkt an.

Hier ist zwar die Länge des Körpers relativ groß, trotzdem ist die Fliehkraft an seinem einen Ende nur sehr wenig von der am anderen Ende abweichend.

Anders beim Gravitationsfeld:

Bei dem Satelliten ist das Gravitationsfeld der Erde nicht homogen, das heißt, dass bei einem großen Satelliten der Teil,  der der Erde näher ist, schwerer ist und der der Erde abgewandte, leichter. Hier greift die Gravitationskraft auch nicht im Schwerpunkt an, sondern im Gravizentrum.  Das wird oft sogar zur Ausrichtung der Satelliten genutzt.

Bei unseren Rotorblättern ist die Drehzahl sehr hoch und der Massenschwerpunkt sehr nahe an der Rotationsachse. Gleichzeitig ist die Ausdehnung des Körpers, der um die Achse dreht, sehr groß im Vergleich zum Abstand zur Rotationsachse.

Die Fliehkraft ist an dem einen Ende fast Null, weil es recht nahe an der Rotationsachse liegt, und am anderen Ende sehr groß, weil es deutlich entfernt von der Achse liegt und sich mit hoher Drehfrequenz um die Achse dreht.

Hier ist der Rechtecksanteil zu vernachlässigen und es überwiegt der Dreiecksanteil der Kurve. Daher greift hier die Fliehkraft nicht im Schwerpunkt, sondern näherungsweise bei 2/3 der Länge der Blätter an.

Dazu werde ich noch einen Versuchsaufbau machen und versuchen meine Behauptung auch zu beweisen.

Nachtrag 02.10.2018

Der Versuch ist nun hier zu finden. Dabei habe ich festgestellt, dass zwar die Fliehkraft (logischerweise) außen größer als innen ist, aber auch, dass es davon abhängt, welche Anordnung der Blätter zur Drehachse betrachtet wird.

Nur in der Schlagbewegung greift die Resultierende nicht im Schwerpunkt an.

In der Schwenkbewegung wirkt die Fliehkraft an jeder Stelle des Blattes noch in unterschiedliche Richtungen, so dass die Summe aller dieser Kräfte bzw. der Normalenanteile davon im Schwerpunkt liegt.

nochmal zurück zur Gravitationskraft

Hier sieht es eigentlich ähnlich aus, mit dem Unterschied, dass die sich Gravitationskraft quadratisch über die Länge des Körpers verändert.

Hierzu gibt es aber bereits viel Info im Internet, so dass ich das hier nicht weiter vertiefen möchte.

Nur soviel: dass die Resultierende nicht im Schwerpunkt angreift, sondern näher zur anderen Masse hin verschoben ist, wird zur Ausrichtung von Satelliten bei ihrem Flug um die Erde genutzt. Der Punkt in dem die Gravitationskräfte angreifen heißt Gravizentrum. Wie man den der Fliehkraft bezeichnet, weiß ich nicht. 

Unwucht

Wenn wir jetzt die Blätter gut gewuchtet sind, also die Wippe gut im Gleichgewicht ist, entstehen auch Fliehkräfte, die sehr gut im Gleichgewicht sind.

Da wir in der Realität aber nie den Idealzustand erreichen können, wird immer ein Unterschied zwischen den Kräften sein, den wir aber z-B. auf der Blattwaage gar nicht feststellen können, weil die Blätter dort auf einer sehr empfindlich eingestellten Waage im Gleichgewicht sind.

Wie weiter oben gelernt, kann ja ein leichtes Gewicht, welches weiter außen liegt, ein schweres , weiter innen liegendes, ausgleichen.

Unbewusst machen wir genau das. Die Vorrichtungen, die wir zum Wuchten benutzen, aber auch meine Excel-Berechnung, machen immer Fehler.

Selbst die feinst eingestellte Blattwaage hat noch Reibungen. Am Ende bleiben immer irgendwelche Unterschiede in den Blättern.

Die führen nun dazu, dass die Fliehkräfte eben nicht genau gleich groß sind. Unterschiedliche Fliehkräfte führen zwangsläufig zur Unwucht.

Manche Methoden suggerieren aber auch, dass gut gewuchtet wurde, weil die Blätter am Ende auf der Blattwaage ausbalanciert sind.

Da wir aber die Schwerpunktlagen nicht genau kennen, kann es eben sein, dass die Schwerpunkte in der Realität weiter auseinander liegen, als wir das erwarten. Je größer dieser Fehler, desto größer auch der Effekt 1 und desto größer wieder die Unwuchten am Rotorkopf.

Zur Unwucht gibt es viel Information im Netz, weshalb ich hier nur die wichtigsten Punkte nochmal aufführen möchte.

to be contiuned